In this article, we will look at how Labouchère and Reverse Labouchère systems work and conduct a mathematical analysis to find out if the 33% win rate is really enough.
First, let us take a step back in history. The strategy was invented by Henry Labouchère (hence the name) who used it for horse racing. However, it is also applicable to roulette and sports betting. Alternatively, the method is called Split Martingale.
The Essence of the Method
In this strategy, the algorithm of actions is the following:
- Decide on the amount you want to win.
Suppose, it is $100. - Divide the amount into several parts. There is no rule as to what parts the amount should be divided into. The only requirement is that the sum of all the parts must equal the amount of your desired winnings.
Suppose, you divided the amount into five equal parts: 20 20 20 20 20 - Now take the leftmost and the rightmost values, add them together and bet the resulting amount with odds no less than 2.0.
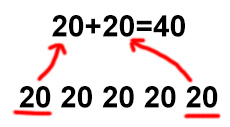
- If you lose your bet, add the lost amount to the end of the row.
20 20 20 20 20 40
In case of a win, remove the values from the row.
2020 20 2020 - Repeat the cycle described in item 3 until all the numbers are crossed out of the row.
Is Labouchère Strategy Effective?
Now let us remember our school Math lessons and try to analyze the information we received:
- To win the desired amount, we need to remove the whole sequence of numbers
- After every loss, one number is added to the row
- After every win, two numbers are removed from the row,
Consequently, we need to have at least 33.4% of wins to close the row and therefore win the desired amount.
Below is the mathematical formula reflecting this principle:
(NumberOfLosses + QuantityOfNumbersInARow) / 2 ≤ NumberOfWins
To illustrate how the formula works, we will use the example above where we had 5 numbers in the row. Suppose, we have already lost one bet. To complete the cycle, we need to win:
(1+5) / 2 = 3 times. Check it
| Row | Event | Bet | Bank |
|---|---|---|---|
| 20 20 20 20 20 | Loss | 20+20 | -40 |
| 20 20 20 20 20 40 | Win | 20+40 | -40+60 =20 |
| 20 20 20 20 | Win | 20+20 | 20+40 =60 |
| 20 20 | Win | 20+20 | 60+40=100 |
So, the calculations are right, but where are the promised 33.4% of wins? According to the table, the ratio is different: 75% of wins against 25% of losses.
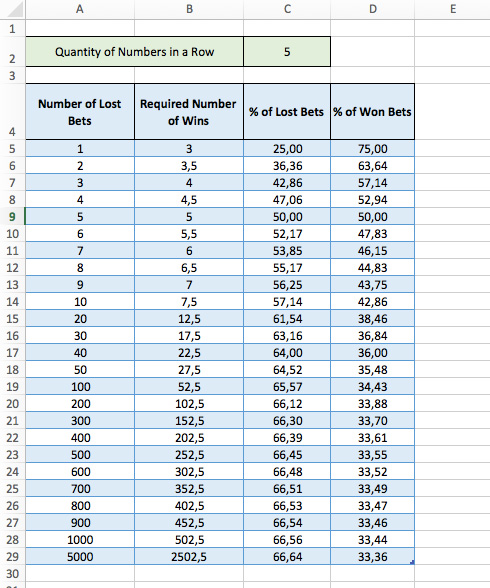
Using the above formula, I created a table in Excel allowing to see these dynamics:
It turns out that the idea with the 33% is the following: the more losses you have, the less wins you need, but not less than 33.34%.
The results in the table are unexpected, and you will not find this information on other websites:
The 33.34% win rate turned out to be nothing more than a theoretical value… almost impossible to reach…
The upside of Labouchère is that, in case of a prolonged losing streak, the losses are significantly less than what they would be with Martingale system.
However, just like in martingale, you still face the question of whether your bankroll is enough to deal with a long losing streak. Besides, do not forget that in real life the percentage of winnings should be higher than 33.34%.
Reverse Labouchère
In Reverse Labouchère, as opposed to regular one, you do everything in reverse:
- In case of a loss, you cross the rightmost and leftmost numbers out of the sequence.
- In case of a win, you add them to the row.
The idea of regular Labouchère is to define the amount you want to win,
while in Reverse Labouchère you define the amount you can afford to lose.
Here is an example. Suppose, you can afford to lose $100.
| Row | Event | Bet | Bank |
|---|---|---|---|
| 20 20 20 20 20 | Loss | 20+20 | 100-40=60 |
| 20 20 20 | Loss | 20+20 | 60-40=20 |
| 20 | Win | 20 | 20+20=40 |
| 20 20 | Win | 20+20 | 40+40=80 |
| 20 20 40 | Win | 20+40 | 80+60=140 |
The game continues until you either lose the amount you initially defined or reach the bet amount that you consider as maximum. In our example, it is $60.
To define the win/loss ratio allowing to get positive ROI, you may use the following formula:
(NumberOfWins + QuantityOfNumbersInARow) ≤ NumberOfLosses * 2
As you can see from the formula, a bettor will lose the game only if he loses more than 33.34% of the bets.
The strategy allows for bigger winnings, but the risks rise accordingly.