Contents
In this article, we will talk about what you need to know about Oscar’s Grind system, explain its rules on a real-life example, see when Oscar’s Grind strategy can be beneficial in sports betting, discuss its pros and cons.
The Basics of the Strategy
The Oscar’s Grind theory is in fact a modified version of Martingale. Except that in Martingale, we need to increase the bet amount when a bet is lost, while in Grind strategy, we are supposed to increase the bet after a win.
For the strategy to work:
- The odds must be no less than 2.0.
- The first bet must make a maximum 1/12 of the bankroll. Otherwise, you risk losing all your bank in a very short time.
The Rules of Oscar’s Grind System on an Example
Let’s assume your first bet is 100 dollars while your bank is 1,200 dollars.
- If your first bet wins, you must double the amount and bet 200 dollars. If your second bet is unlucky, the cycle is over. Your bank is: 1,200+100+200=1,500 dollars. Then you need to start a new cycle lowering the bet amount to 100 dollars.
- If both the first and the second bets lose, the bet amount remains the same. The next bet, just like the previous one, must be 100 dollars.
| Bet # | Bet Amount | Outcome | Balance |
|---|---|---|---|
| Bet 1 | 100 | Loss | 1200-100 = $1100 |
| Bet 2 | 100 | Loss | 1100-100 = $1000 |
| Bet 3 | 100 | Loss | 1000-100 = $900 |
| Bet 4 | 100 | Win | 900+100 = $1000 |
| Bet 5 | 200 | Win | 1000+200 = $1200 |
| Bet 6 | 100 | Win | 1200+100 = $1300 |
As is shown in the table, to earn profit, 3 out of 6 (that is, a half) of our bets must win.
Oscar’s Grind Strategy in practice. Case Study
Instead of reading online reviews, we will try the strategy in a real-life situation.
Given: a deposit of 1,500 dollars.
We pick the English Premier League club Newcastle and choose the right odds. Let it be ‘both teams to score — no’, because, in this case, we can count on the odds we need — a little more than 2.
Bet 1. We bet 100 dollars with odds of 2.15.
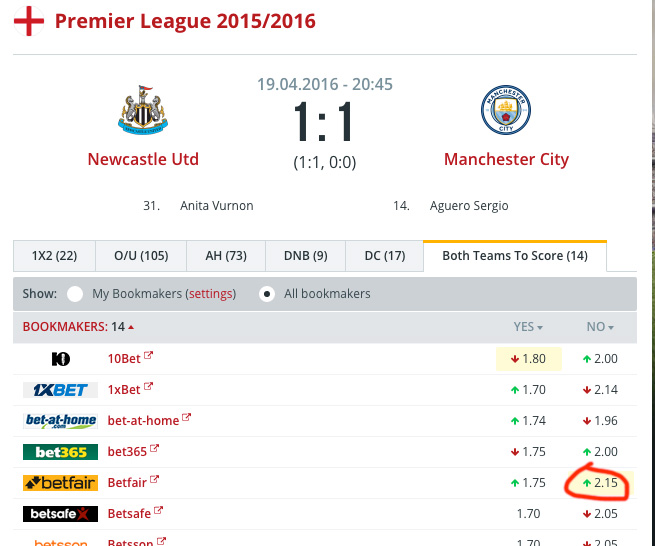
And lose. The current balance is: $1,500 — $100 = $1,400
Bet 2. According to the strategy rules, our second bet is $100 with the same odds of 2.15.
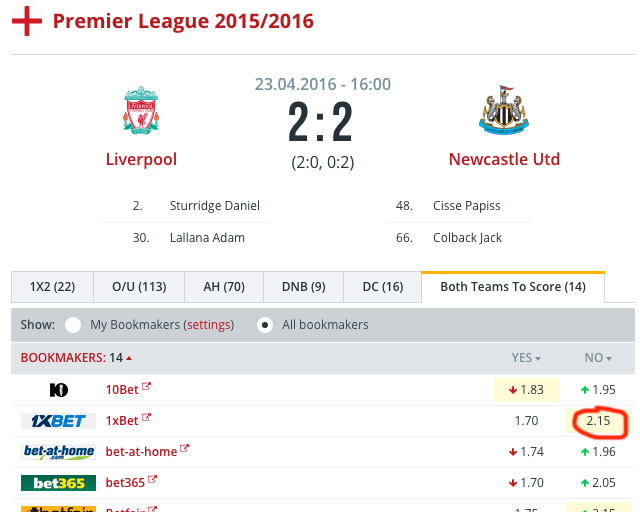
We lose again. The current balance is: $1,400 — $100 = $1,300
Bet 3. $100 with odds of 2.12.
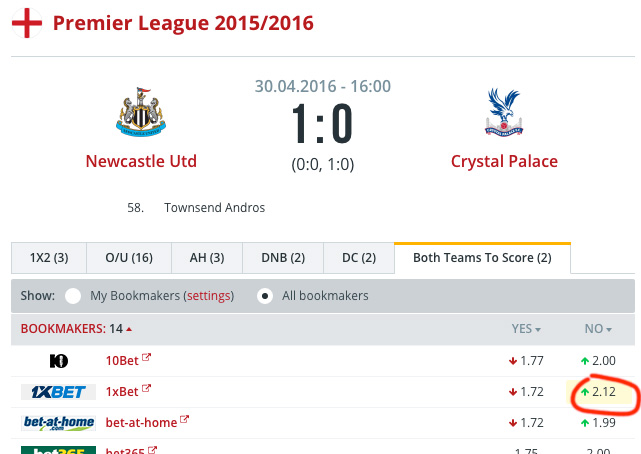
This time we have more luck and win 112 dollars. The current balance is: $1,300 + $112 = $1,412
Bet 4. Following the rules of Oscar’s Grind system, we increase the previous bet by exactly two times: $200 with odds 2.05.
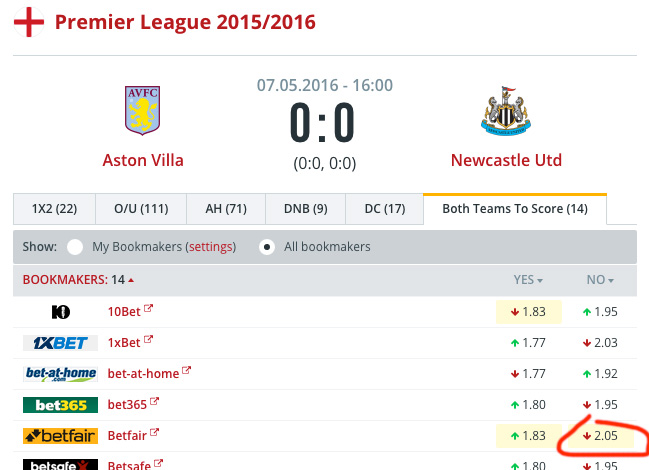
We win again. The current balance is: $1,412 + $210 = $1,622
Resume: 1,500-100-100+112+210=1,622 dollars. As you can see, our net profit is 122 dollars.
However, there is a fly in the ointment. If we continued to play with the strategy, already in the next game Newcastle-Tottenham (that ended with the lopsided score of 1-5) we would have lost almost all our winnings.
Resume. Can You Win with the Oscar’s Grind Strategy? Reviews
So, can you win with the Oscar’s Grind method? In the short run, if you very lucky, yes, you can. However, if you plan to use the strategy long-term, it will slowly but steadily drain your bankroll.
For the system to win, the success rate of your bets must be 50%.
According to the probability theory, this is hardly possible, as the strategy rules require that the odds for your bets must always be higher than 2.0.
If the above statement is not quite clear, read this article and it will break it all down for you.
Can you be certain that you are more an expert than the bookmaker team and that you will be able to turn the situation in your favor? Right, you can’t. Even if you keep on winning for a while, it won’t be long before you hit a rough patch and your balance tends to zero.
At some point, the Oscar’s Grind strategy can be useful, but don’t get carried away with it.
The one big advantage of the strategy is that you will hardly face the issue of bookmaker limitations. It will also prevent you from quickly draining your bankroll, keep your excitement up and let you play longer.
Don’t rely on luck only. Do a thorough analysis of the event every time before you bet.





 (2 votes, average: 4.50 out of 5)
(2 votes, average: 4.50 out of 5)